Zeiss 15/2.8 Distagon Q&A — Lens Construction

2012-03-19 • SEND FEEDBACK •
Related: longitudinal chromatic aberration, optics, secondary longitudinal chromatic aberration, wide angle, Zeiss, Zeiss 15mm f/2.8 Distagon, Zeiss Distagon, Zeiss DSLR Lenses, Zeiss Lenses

ZF.2 15mm f/2.8 Distagon T*

A review of the ZEISS 15mm f/2.8 Distagon and other ZEISS ZF/ZE lenses can be found in the diglloyd Guide to Zeiss ZF / ZE Lenses.

This is one of several pages resulting from the March 13, 2012 discussion with Staff Scientist Dr. Hubert Nasse. See the original list of questions.

These pages are a summary of the discussion based on notes taken, and as reviewed by Dr. Nasse. Bracketed comments [ ] are editorial in nature.

Among its 15 elements, the 15/2.8 Distagon uses two aspheric elements, and five (5) anomalous partial dispersion elements (Nikon calls these “ED” and “Super ED”).

When focusing, the rear group behind the iris moves, changing the spacing behind the iris.

The optical calculation assumes a sensor cover glass thickness of an average thickness for most Nikon and Canon DSLR camera bodies.

Two aspheric lens elements

The two aspheric elements are used primarily to control distortion, and also field curvature.

The 2nd (from front) lens element is aspheric on its subject-facing surface. The rear lens element is aspheric on its camera-facing surface.

A front aspheric element would have been preferred, but due to its large size, such a choice would have raised the cost substantially due to higher production costs to achieve the required precision over such a large area.

Use of aspheric elements in ZEISS ZF.2 15mm f/2.8 Distagon T*

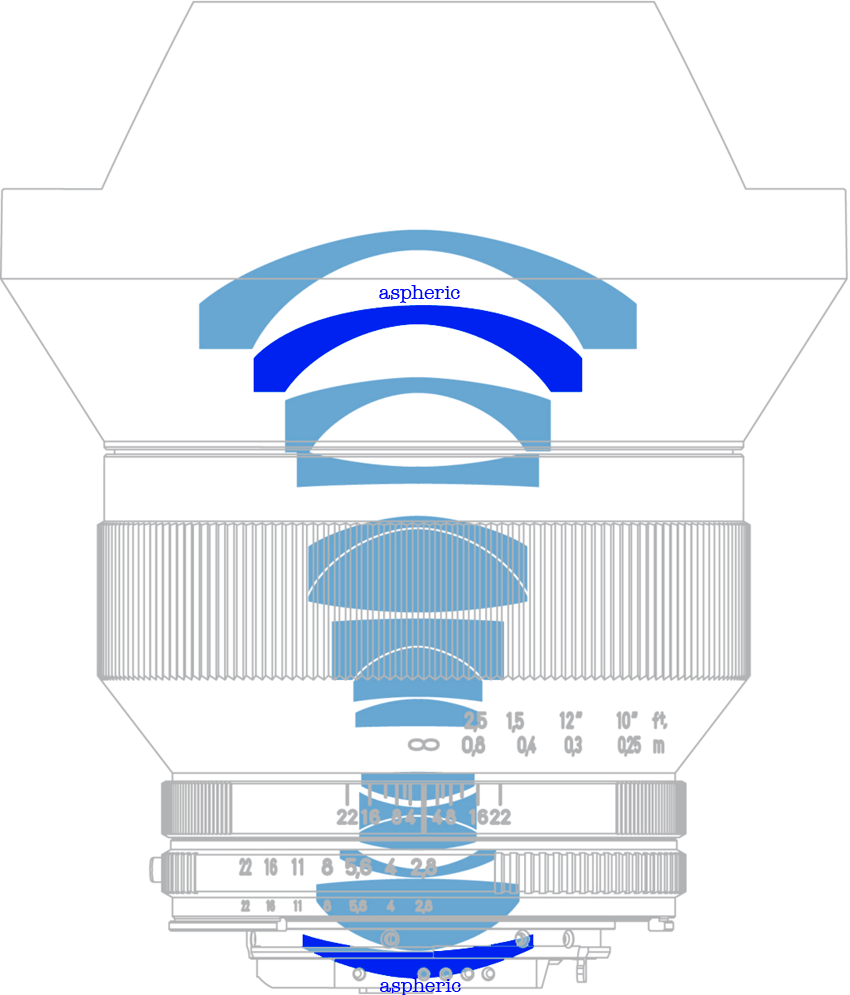
Anomalous partial dispersion elements

Anomalous partial dispersion* glass has a non-linear refraction of color wavelengths, making it possible to combine different glass types for a desired level of color correction.

The refractive properties are only a factor of 5 different. Were there a magical type of glass with 10X more refractive power, that would would be lovely, but such glass does not exist; it is always a combination of glass types to solve the design challenges.

Such glass types are often more expensive and are thus used sparingly unless needed. Moreover, use of such special glass types often requires a careful choreographing with other elements of special type, to balance the total behavior.

In the 15/2.8 Distagon, there are five (5) anomalous partial dispersion elements with refractive indices ranging from 1.43 to 1.85. Their differing and complementary dispersion (refraction) characteristics are used in a complex interplay to achieve the high performance and superb correction of color errors.

The five glasses with anomalous dispersion have all low index of 1.5 and lower; above figures 1.43 and 1.84 refer to the total range of refractive index.

The 15/2.8 Distagon optical performance in such a relatively compact lens would not have been possible without a wide range of glass types to choose from.

* Nikon has the convenient of ED (extra-low dispersion) and Super ED glass.

Dr. Nasse explains:

The two most important glass parameters, also displayed in the standard glass charts, are the refractive index and the Abbe number.

The refractive index of optical glass ranges between about 1.45 and 2, and it describes the refractive power of the glass for a single wavelength, usually green light.

The Abbe number describes the basic dispersion properties of the glass, so how the refractive index changes with the color of light. The Abbe number has a very practical meaning: for a single lens it tells us how large the longitudinal focal difference is between red and blue light, expressed as a fraction of the focal length of that lens. Abbe numbers of optical glass range between about 20 (high dispersion) and 100 (low dispersion).

For a somehow useful achromatic lens combination the longitudinal color aberration should however be as low as 1/1000 of the focal length. This teaches us, that not the low refractive index of these special glasses is there most important feature. Not a single existing glass has low enough dispersion to be good enough for our purposes – it is always a matter of combining glasses to achieve satisfying compensation. And the useful feature of the glass types with anomalous partial dispersion is that they allow for a better matching to the dispersion curves of their higher index partners.

You can compare color correction to the matching of two curves in a graph: if you want to make two straight lines be coincident in the graph, you introduce a second vertical axis, assign one line to the left side axis, the other to the right side. Then you can independently select the scale length and the zero position on left and right vertical axis, and this can make all straight lines of different slope perfectly coincident. The selection of vertical scale parameters corresponds in optics to the selection of lens powers by defining the surfaces radius (however with side effects to the monochromatic correction).

Color correction would work perfectly with all glass combinations if nature would have given us material with just strictly linear variation of the refractive power with the wavelength. But to keep us busy nature has decided in a different way: glass dispersion curves ( n over wavelength) are not linear, they are curved, normally more curved the higher the index is. This mismatch of curvatures is the source of secondary spectrum, residual errors of color correction. Glass types with anomalous partial dispersion deviate from the standard laws ‘… more curved the higher…’ and thus they allow a better match of curvatures of the dispersion curves and to reduce by this the secondary spectrum. In the graph you would have the similar trouble: you can’t match two differently curved lines just by variation of the vertical scale parameters, at least as long as the scales themselves maintain equidistant steps.